数字控制器
模拟式PID控制器
一、数字 PID 算法
1. 位置式 PID 算法
稳态精度高
直观易于理解
计算量大
积分饱和
2. 增量式 PID 算法
无积分环节积累,可能存在一定误差
两种 PID 形式的优缺点
3. 一般 PID 算法的离散化
一般常用模拟控制器离散化#二、差分变换法 ,用后向差分,或双线性差分
并写为控制器的形式
二、改进的数字 PID 算法
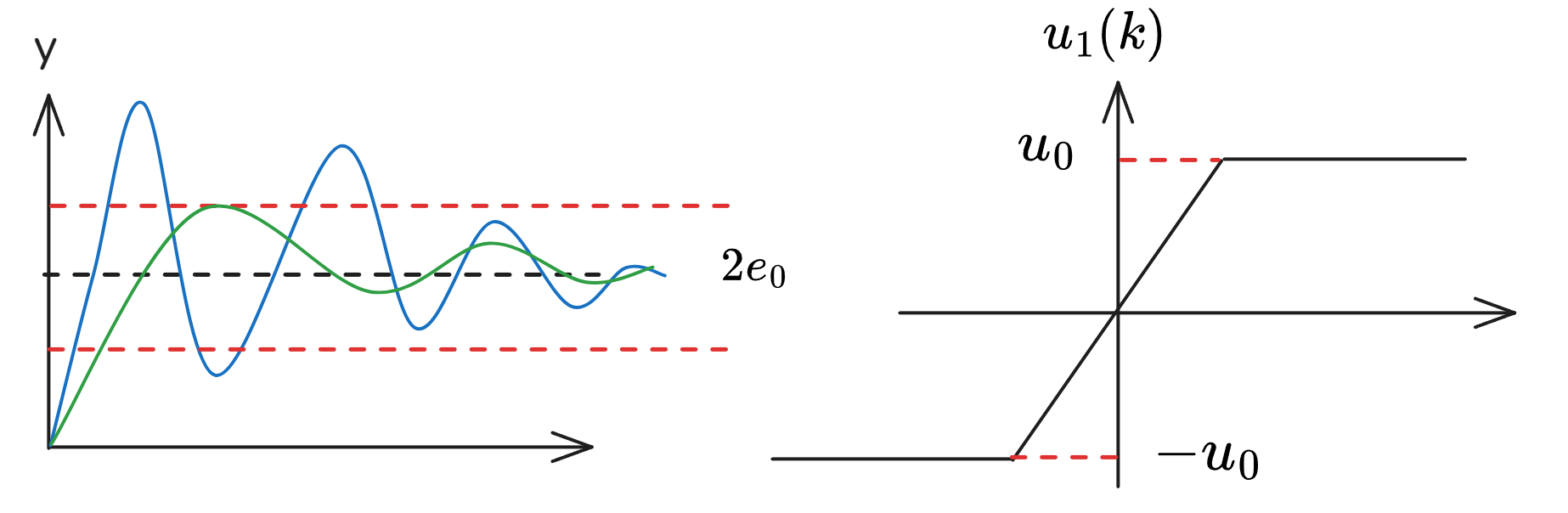
1. 积分分离算法
在系统误差较大时,取消积分作用;当误差减小到一定值时,再重新积分。 为积分分离阈值
采用 PID 控制,保证稳态误差为 0
采用 PD 控制,大幅度减小超调量
抗饱和积分算法
输出限幅,输出超限时不积分
遇限削弱算法
不完全微分
纯微分环节对噪声很敏感
可以串接一个惯性环节来抑制高频影响
微分先行
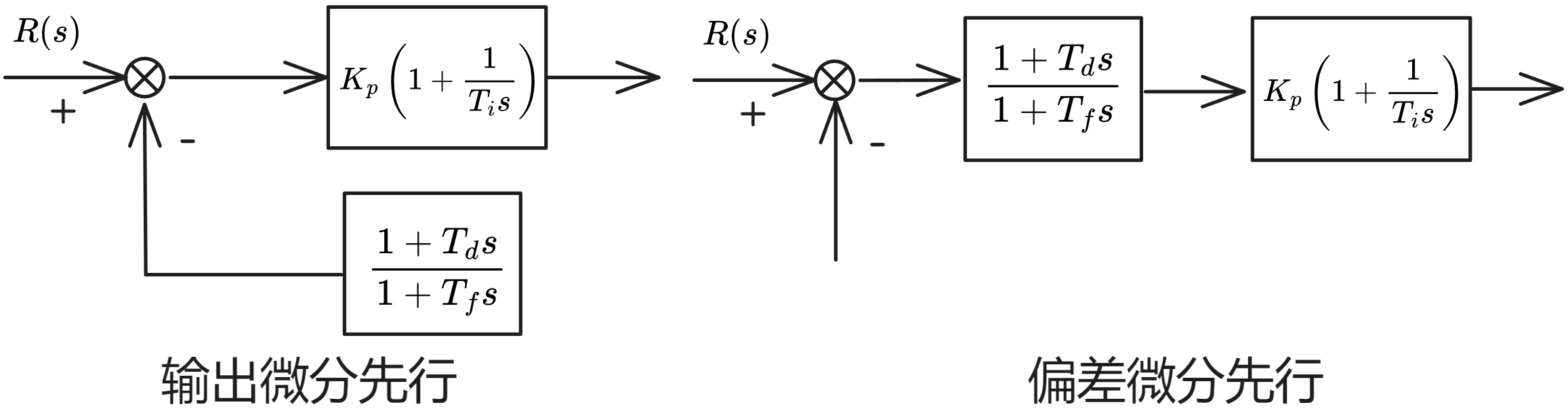
输出量微分:只对输出量进行微分,避免因给定值变化给控制系统带来超调量过大、调节阀动作剧烈的冲击
偏差量微分:对给定值和输出量均微分
控制器的正反作用实现:
反作用:
正作用:
带死区的 PID

